Geometria Espacial

A Geometria Espacial estuda os objetos que possuem mais de uma dimensão e ocupam lugar no espaço. Por sua vez, esses objetos são conhecidos como "sólidos geométricos" ou "figuras geométricas espaciais".
Dessa forma, a geometria espacial é capaz de determinar, por meio de cálculos matemáticos, o volume destes objetos, ou seja, o espaço ocupado por eles. Contudo, o estudo das estruturas das figuras espaciais e suas inter-relações é determinado por alguns conceitos básicos, a saber:

Ponto: conceito fundamental a todos os subsequentes, uma vez que todos sejam, em última análise, formados por inúmeros pontos. Por sua vez, os pontos são infinitos e não possuem dimensão mensurável (adimensional). Portanto, sua única propriedade garantida é sua localização.
Reta: composta por pontos, é infinita nos dois lados e determina a distância mais curta entre dois pontos determinados.
Linha: possui algumas semelhanças com a reta, pois é igualmente infinita para cada lado, contudo, têm a propriedade de formar curvas e nós sobre si mesma. Plano: é outra estrutura infinita que se estende em todas as direções.

Figuras Geométricas Espaciais

Cubo ou Hexaedro Regular é o sólido construído com seis quadrados, assim tendo 12 arestas e 8 vértices.



Diagonal (D) = a√3
Área Total (S) = 6a²
Volume (V) = a.a.a = a³

Paralelepípedo: Paralelepípedo Reto Retângulo é o sólido construído com seis retângulos, congruentes dois a dois, conforme ilustra a figura abaixo.



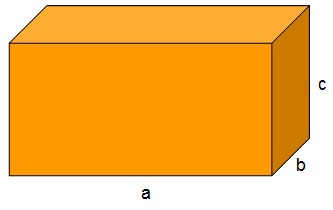
Diagonal (D) = √a² + √b² + √c²
Área Total (S) = 2.(ab + bc + ca)
Volume(V) = a.b.c

Cilíndro circular reto:


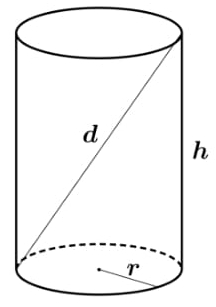
Área da Base = π.r²
Área Lateral = 2π.r.h
Área Total = 2.π.r² + 2π.r.h = 2π.r(r + h)
Volume = π.r².h